11455. K специальных
ячеек
Вам дана матрица, в которой
выделены k специальных ячеек. Вы должны достичь клетку (n, m)
из (1, 1). Из любой клетки можно двигаться только вправо или вниз.
k специальных ячеек – это те ячейки сетки, которые обладают особой силой. i-я
специальная ячейка имеет pi единиц силы, и если Вы проходите по этой ячейке, то приобретаете эту силу.
Найдите общую суммарную силу,
которую Вы можете приобрести после прохождения всех возможных путей в сетке,
чтобы достичь ячейки (n, m).
Отметим, что:
·
Сила пути равна сумме сил pi всех специальных ячеек,
посещенных на этом пути.
·
Ячейки, не являющиеся специальными, имеют силу ноль.
Вход. Первая строка содержит количество тестов t.
Первая строка каждого теста
содержит три целых числа n, m (1 ≤ n, m ≤
105) и k (1 ≤ k ≤ 106), где n ∗ m – размер сетки, а k – общее количество специальных ячеек в
сетке. Каждая из следующих k строк содержит xi, yi (1 ≤ xi ≤ n, 1 ≤
yi ≤ m) и pi
(1 ≤ pi ≤ 105), где (xi,
yi) – расположение специальной
ячейки, а pi – ее сила.
Выход. Для каждого теста выведите в отдельной строке общую силу,
которую Вы можете приобрести. Поскольку общая сила может быть слишком большой,
то выведите ее по модулю 109 + 7.
|
Пример
входа |
Пример
выхода |
|
1 2 2 2 1 2 4 2 1 7 |
11 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Пусть
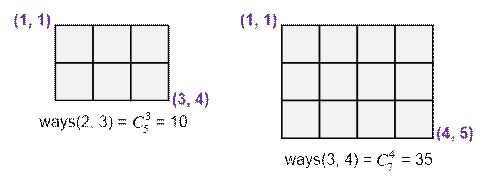
ways(x, y) – количество путей
на матрице из (1, 1) в (1 + x, 1 + y). Тогда
ways(x, y) = 
= 
Количество
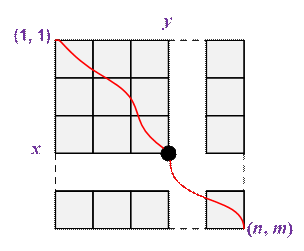
путей из (1, 1) в (n, m), проходящих через специальную ячейку (x, y) равно ways(x – 1, y – 1) * ways(n
– x, m – y). Умножив это значение на p, мы получим суммарную силу
всех путей, проходящих через ячейку (x, y).
Остается
просуммировать силы всех путей, проходящих через все специальные ячейки. Ответ равен
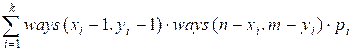
Пример
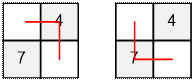
В приведенном примере имеются k
= 2 специальные ячейки.
В точности 1 путь проходит через
ячейку с силой 4.
В точности 1 путь проходит через
ячейку с силой 7.
Поэтому общая сила равна 4 + 7 =
11.
Реализация алгоритма
Объявим массивы:
fact содержит
факториалы чисел по модулю MOD, factinv содержит числа,
обратные факториалам чисел по модулю MOD:
fact[n] = n!
mod 1000000007
factinv[n] = n!
-1 mod 1000000007
#define MAX 800001
ll fact[MAX], factinv[MAX];
Функция pow вычисляет степень числа по модулю: xn mod p.
ll pow(ll x, ll n, ll p)
{
if (n == 0) return 1;
if (n % 2 == 0) return pow((x * x) % p, n / 2, p);
return (x * pow(x, n - 1, p)) % p;
}
Функция inverse находит число, обратоне x по простому модулю
p. Поскольку число p простое, то по
теореме Ферма xp-1 mod p = 1 для всякого 1 ≤ x < p. Равенство можно переписать в виде (x * xp-2) mod p = 1, откуда обратным к x является число
xp-2 mod p.
ll inverse(ll x, ll p)
{
return pow(x, p - 2, p);
}
Функция Cnk вычисляет
биномиальный коэффициент по формуле:
=
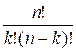
ll Cnk(int n, int k)
{
return ((fact[n] * factinv[k]) % MOD * factinv[n - k]) % MOD;
}
Функция ways вычисляет количество
путей на решетке размером n * m от клетки (0, 0) до клетки (n, m). Поскольку путь
между указанными точками имеет длину n + m, и при этом
содержит m горизонтальных
сегментов, то число путей равно 
.
ll ways(int n, int m)
{
return Cnk(n + m, m);
}
Основная часть программы. Заполняем массивы факториалов fact и factinv.
fact[0] =
1;
for (i = 1; i < MAX; i++)
fact[i] = (fact[i - 1] * i) % MOD;
factinv[0]
= 1;
for (i = 1; i < MAX; i++)
factinv[i] = inverse(fact[i], MOD);
Последовательно обрабатываем tests тестов.
scanf("%d", &tests);
while (tests--)
{
Читаем данные текущего теста.
scanf("%d %d %d", &n, &m, &k);
Общую
приобретенную силу вычисляем в переменной res.
res = 0;
Обрабатываем k специальных ячеек.
for (i = 0; i < k; i++)
{
scanf("%d %d %d", &x, &y, &p);
res = (res + (ways(x - 1, y - 1) *
ways(n - x, m - y)) % MOD * p) % MOD;
}
Выводим ответ для текущего теста.
printf("%lld\n", res);
}